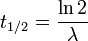Fisika

Waktu Paruh dan Radio Aktif

Rabu, 04 Maret 2015

Isotop uranium menghasilkan plutonium-239 sebagai produk peluruhan. Plutonium dapat digunakan dalam senjata nuklir dan merupakan sumber daya untuk reaktor nuklir, yang menghasilkan listrik. Isotop ini memiliki waktu paruh 24.100 tahun, tentu saja ini menimbulkan kekhawatiran di daerah di mana plutonium radioaktif telah terakumulasi dan disimpan. Pada beberapa situs penyimpanan, limbah secara perlahan bocor ke air tanah dan mencemari sungai di dekatnya. 24.100 tahun waktu paruh berarti bahwa ia akan bersama kita untuk waktu yang sangat lama.

Waktu Paruh

Bahan radioaktif kehilangan sebagian dari aktivitas mereka setiap kali terjadi peristiwa peluruhan. Hilangnya aktivitas dapat diperkirakan dengan menentukan waktu paruh isotop. Waktu paruh Didefinisikan sebagai periode waktu yang diperlukan untuk setengah dari jumlah tertentu dari suatu zat untuk mengalami perubahan. Untuk radioisotop, setiap kali peristiwa peluruhan terjadi, jumlahnya akan terdeteksi pada Geiger counter atau alat pengukur lainnya. Sebuah isotop tertentu mungkin memiliki jumlah total 30.000 BPJ. Dalam satu jam, jumlah bisa 15.000 BPJ (setengah jumlah aslinya). Jadi waktu paruh isotop yang satu jam. Beberapa isotop memiliki waktu paruh yang panjang – waktu paruh U-234 adalah 245.000 tahun. Isotop lain memiliki waktu paruh yang lebih pendek. I-131, yang digunakan dalam scan tiroid, memiliki waktu paruh 8.02 hari.

Perhitungan Waktu Paruh

Informasi tentang waktu paruh isotop dapat digunakan untuk menghitung berapa banyak radioaktivitas isotop yang akan hadir setelah jangka waktu tertentu. Ada rumus yang memungkinkan perhitungan setiap saat setelah menghitung dari awal, tetapi kita hanya akan melihat hilangnya aktivitas setelah waktu paruh yang berbeda. Isotop I-125 digunakan dalam prosedur laboratorium tertentu dan memiliki waktu paruh 59,4 hari. Jika aktivitas awal sampel I-125 adalah 32.000 BPJ, berapa banyak aktivitas akan hadir setelah 178,2 hari? Kita mulai dengan menentukan berapa banyak waktu paruh yang dialami setelah 178,2 hari:

(178.2 hari/59,4hari) = 3 kali waktu paruh

Kemudian kita hitung aktivitasnya:

Keadaan awal (t_o) = 32.000 BPJ

Setelah satu kali waktu paruh = 16.000 BPJ

Setelah dua kali waktu paruh = 8.000 BPJ

Setelah tiga kali waktu paruh = 4.000 BPJ

Pastikan untuk diingat bahwa jumlah awal adalah pada waktu nol (t = 0) dan kita kurangi dari jumlah pertama waktu paruh. Paruh kedua memiliki aktivitas setengah dari perhitungan sebelumnya (bukan hitungan awal).

Bagi yang lebih cenderung matematis, rumus berikut dapat digunakan untuk menghitung jumlah radioaktivitas yang tersisa setelah waktu tertentu:

N_t = N_o x (0,5)^{n (t ½ )}

Dengan N_t = aktivitas setelah waktu t

N_o = aktivitas awal saat t = 0

RADIO AKTIF

Radioaktivitas pertama kali ditemukan pada tahun 1896 oleh ilmuwan Perancis Henri Becquerel ketika sedang bekerja dengan material fosforen. Material semacam ini akan berpendar di tempat gelap setelah sebelumnya mendapat paparan cahaya, dan dia berfikir pendaran yang dihasilkan tabung katode oleh sinar-X mungkin berhubungan dengan fosforesensi. Karenanya ia membungkus sebuah pelat foto dengan kertas hitam dan menempatkan beragam material fosforen diatasnya. Kesemuanya tidak menunjukkan hasil sampai ketika ia menggunakan garam uranium. Terjadi bintik hitam pekat pada pelat foto ketika ia menggunakan garam uranium tesebut.

Tetapi kemudian menjadi jelas bahwa bintik hitam pada pelat bukan terjadi karena peristiwa fosforesensi, pada saat percobaan, material dijaga pada tempat yang gelap. Juga, garam uranium nonfosforen dan bahkan uranium metal dapat juga menimbulkan efek bintik hitam pada pelat.

Partikel Alfa tidak mampu menembus selembar kertas, partikel beta tidak mampu menembus pelat alumunium. Untuk menghentikan gamma diperlukan lapisan metal tebal, namun karena penyerapannya fungsi eksponensial akan ada sedikit bagian yang mungkin menembus pelat metal

Pada awalnya tampak bentuk radiasi yang baru ditemukan ini mirip dengan penemuan sinar-X. Akan tetapi, penelitian selanjutnya yang dilakukan oleh Becquerel, Marie Curie, Pierre Curie, Ernest Rutherford dan ilmuwan lainnya menemukan bahwa radiaktivitas jauh lebih rumit ketimbang sinar-X. Beragam jenis peluruhan bisa terjadi.

Sebagai contoh, ditemukan bahwa medan listrik atau medan magnet dapat memecah emisi radiasi menjadi tiga sinar. Demi memudahkan penamaan, sinar-sinar tersebut diberi nama sesuai dengan alfabet yunani yakni alpha, beta, dan gamma, nama-nama tersebut masih bertahan hingga kini. Kemudian dari arah gaya elektromagnet, diketahui bahwa sinar alfa mengandung muatan positif, sinar beta bermuatan negatif, dan sinar gamma bermuatan netral. Dari besarnya arah pantulan, juga diketahui bahwa partikel alfa jauh lebih berat ketimbang partikel beta. Dengan melewatkan sinar alfa melalui membran gelas tipis dan menjebaknya dalam sebuah tabung lampu neon membuat para peneliti dapat mempelajari spektrum emisi dari gas yang dihasilkan, dan membuktikan bahwa partikel alfa kenyataannya adalah sebuah inti atom helium. Percobaan lainnya menunjukkan kemiripan antara radiasi beta dengan sinar katode serta kemiripan radiasi gamma dengan sinar-X.

Para peneliti ini juga menemukan bahwa banyak unsur kimia lainnya yang mempunyai isotop radioaktif. Radioaktivitas juga memandu Marie Curie untuk mengisolasi radium dari barium; dua buah unsur yang memiliki kemiripan sehingga sulit untuk dibedakan.

Bahaya radioaktivitas dari radiasi tidak serta merta diketahui. Efek akut dari radiasi pertama kali diamati oleh insinyur listrik Amerika Elihu Thomson yang secara terus menerus mengarahkan sinar-X ke jari-jarinya pada 1896. Dia menerbitkan hasil pengamatannya terkait dengan efek bakar yang dihasilkan. Bisa dikatakan ia menemukan bidang ilmu fisika medik (health physics); untungnya luka tersebut sembuh dikemudian hari.

Efek genetis radiasi baru diketahui jauh dikemudian hari. Pada tahun 1927 Hermann Joseph Muller menerbitkan penelitiannya yang menunjukkan efek genetis radiasi. Pada tahun 1947 dimendapat penghargaan hadiah Nobel untuk penemuannya ini.

Sebelum efek biologi radiasi diketahui, banyak perusahan kesehatan yang memasarkan obat paten yang mengandung bahan radioaktif; salah satunya adalah penggunaan radium pada perawatan enema. Marie Curie menentang jenis perawatan ini, ia memperingatkan efek radiasai pada tubuh manusia belum benar-benar diketahui (Curie dikemudian hari meninggal akibat Anemia Aplastik, yang hampir dipastikan akibat lamanya ia terpapar Radium). Pada tahun 1930-an produk pengobatan yang mengandung bahan radioaktif tidak ada lagi dipasaran bebas.

Mode Peluruhan[sunting | sunting sumber]

Sebuah inti radioaktif dapat melakukan sejumlah reaksi peluruhan yang berbeda. Reaksi-reaksi tersebut disarikan dalam tabel berikut ini. Sebuah inti atom dengan muatan (nomor atom) Z dan berat atom A ditampilkan dengan (A, Z).

Mode peluruhan	Partikel yang terlibat	Inti anak
Peluruhan dengan emisi nukleon:
Peluruhan alfa	Sebuah partikel alfa (A=4, Z=2) dipancarkan dari inti	(A-4, Z-2)
Emisi proton	Sebuah proton dilepaskan dari inti	(A-1, Z-1)
Emisi neutron	Sebuah neutron dilepaskan dari inti	(A-1, Z)
Fisi spontan	Sebuah inti terpecah menjadi dua atau lebih atom dengan inti yang lebih kecil disertai dengan pemancaran partikel lainnya	-
Peluruhan cluster	Inti atom memancarkan inti lain yang lebih kecil tertentu (A₁, Z₁) yang lebih besar daripada partikel alfa	(A-A₁, Z-Z₁) + (A₁,Z₁)
Berbagai peluruhan beta:
Peluruhan beta	Sebuah inti memancarkan elektron dan sebuah antineutrino \|\| (A, Z+1)
Emisi positron	Sebuah inti memancarkan positron dan sebuah neutrino	(A, Z-1)
Tangkapan elektron	Sebuah inti menangkap elektron yang mengorbit dan memancarkan sebuah neutrino	(A, Z-1)
Peluruhan beta ganda	Sebuah inti memancarkan dua elektron dan dua antineutrinos	(A, Z+2)
Tangkapan elektron ganda	Sebuah inti menyerap dua elektron yang mengorbit dan memancarkan dua neutrino	(A, Z-2)
Tangkapan elektron dengan emisi positron	Sebuah inti menangkap satu elektron yang mengorbit memancarkan satu positron dan dua neutrino	(A, Z-2)
Emisi positron ganda	Sebuah inti memancarkan dua positrons dan dua neutrino	(A, Z-2)
Transisi antar dua keadaan pada inti yang sama:
Peluruhan gamma	Sebuah inti yang tereksitasi melepaskan sebuah foton energi tinggi (sinar gamma)	(A, Z)
Konversi internal	Inti yang tereksitasi mengirim energinya pada sebuah elektron orbital dan melepaskannya	(A, Z)

Peluruhan radioaktif berakibat pada pengurangan massa, dimana menurut hukum relativitas khusus massa yang hilang diubah menjadi energi (pelepasan energi) sesuai dengan persamaan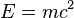

E = mc^2

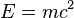. Energi ini dilepaskan dalam bentuk energi kinetik dari partikel yang dipancarkan.

Rantai peluruhan dan mode peluruhan ganda[sunting | sunting sumber]

Banyak inti radioaktif yang mempunyai mode peluruhan berbeda. Sebagai contoh adalah Bismuth-212, yang mempunyai tiga.

Inti anak yang dihasilkan dari proses peluruhan biasanya juga tidak stabil, kadang lebih tidak stabil dari induknya. Bila kasus ini terjadi, inti anak tadi akan meluruh lagi. Proses kejadian peluruhan berurutan yang menghasilkan hasil akhir inti stabil, disebut rantai peluruhan.

Keberadaan dan penerapan[sunting | sunting sumber]

Menurut teori Big Bang, isotop radioaktif dari unsur teringan (H, He, dan Li) dihasilkan tidak berapa lama seteleah alam semesta terbentuk. Tetapi, inti-inti ini sangat tidak stabil sehingga tidak ada dari ketiganya yang masih ada saat ini. Karenanya sebagian besar inti radioaktif yang ada saat ini relatif berumur muda, yang terbentuk di bintang (khususnyasupernova) dan selama interaksi antara isotop stabil dan partikel berenergi. Sebagai contoh, karbon-14, inti radioaktif yang mempunyai umur-paruh hanya 5730 tahun, secara terus menerus terbentuk di atmosfer atas bumi akibat interaksi antara sinar kosmik dan Nitrogen.

Peluruhan radioaktif telah digunakan dalam teknik perunut radioaktif, yang digunakan untuk mengikuti perjalanan subtansi kimia di dalam sebuah sistem yang kompleks (sepertiorganisme hidup misalnya). Sebuah sampel dibuat dengan atom tidak stsbil konsentrasi tinggi. Keberadaan substansi di satu atau lebih bagian sistem diketahui dengan mendeteksi lokasi terjadinya peluruhan.

Dengan dasar bahwa proses peluruhan radioaktif adalah proses acak (bukan proses chaos), proses peluruhan telah digunakan dalam perangkat keras pembangkit bilangan-acak yang merupakan perangkat dalam meperkirakan umur absolutmaterial geologis dan bahan organik.

Laju peluruhan radioaktif[sunting | sunting sumber]

Laju peluruhan, atau aktivitas, dari material radioaktif ditentukan oleh:

Konstanta:

Waktu paruh - simbol 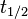$t_{1/2}$ - waktu yang diperlukan sebuah material radioaktif untuk meluruh menjadi setengah bagian dari sebelumnya.
Rerata waktu hidup - simbol $\tau$ - rerata waktu hidup (umur hidup) sebuah material radioaktif.
Konstanta peluruhan - simbol $\lambda$ - konstanta peluruhan berbanding terbalik dengan waktu hidup (umur hidup).

(Perlu dicatat meskipun konstanta, mereka terkait dengan perilaku yang secara statistik acak, dan prediksi menggunakan kontanta ini menjadi berkurang keakuratannya untuk material dalam jumlah kecil. Tetapi, peluruhan radioaktif yang digunakan dalam teknik penanggalan sangat handal. Teknik ini merupakan salah satu pertaruhan yang aman dalam ilmu pengetahuan sebagaimana yang disampaikan oleh [1])

Variabel:

Aktivitas total - simbol $A$ - jumlah peluruhan tiap detik.
Aktivitas khusus - simbol $S_A$ - jumlah peluruhan tiap detik per jumlah substansi. "Jumlah substansi" dapat berupa satuan massa atau volume.)

Persamaan:

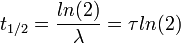
t_{1/2} = \frac{ln(2)}{\lambda} = \tau ln(2)

A = \frac{dN}{dt} = - \lambda N

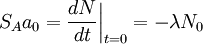
S_A a_0 = \frac{dN}{dt}\bigg|_{t=0} = - \lambda N_0

dimana

a_0 \

adalah jumlah awal material aktif.

Pengukuran aktivitas[sunting | sunting sumber]

Satuan aktivitas adalah: becquerel (simbol Bq) = jumah disintegrasi (pelepasan)per detik ; curie (Ci) =

3.7 \times 10^{10} \

disintegrasi per detik; dan disintegrasi per menit (dpm).

Waktu peluruhan[sunting | sunting sumber]

Sebagaimana yang disampaikan di atas, peluruhan dari inti tidak stabil merupakan proses acak dan tidak mungkin untuk memperkirakan kapan sebuah atom tertentu akan meluruh, melainkan ia dapat meluruh sewaktu waktu. Karenanya, untuk sebuah sampel radioisotop tertentu, jumlah kejadian peluruhan –dN yang akan terjadi pada selang (interval) waktu dt adalah sebanding dengan jumlah atom yang ada sekarang. Jika N adalah jumlah atom, maka kemungkinan (probabilitas) peluruhan (– dN/N) sebanding dengan dt:

\left(-\frac{dN}{N} \right) = \lambda \cdot dt

Masing-masing inti radioaktif meluruh dengan laju yang berbeda, masing-masing mempunyai konstanta peluruhan sendiri (λ). Tanda negatif pada persamaan menunjukkan bahwa jumlah N berkurang seiring dengan peluruhan. Penyelesaian dari persamaan diferensial orde 1 ini adalah fungsi berikut:

N(t) = N_0 e^{-\lambda t} \,\!

Fungsi di atas menggambarkan peluruhan exponensial, yang merupakan penyelesaian pendekatan atas dasar dua alasan. Pertama, fungsi exponensial merupakan fungsi berlanjut, tetapi kuantitas fisik N hanya dapat bernilai bilangan bulat positif. Alasan kedua, karena persamaan ini penggambaran dari sebuah proses acak, hanya benar secara statistik. Akan tetapi juga, dalam banyak kasus, nilai N sangat besar sehingga fungsi ini merupakan pendekatan yang baik.

Selain konstanta peluruhan, peluruhan radioaktif sebuah material biasanya juga dicirikan oleh rerata waktu hidup. Masing-masing atom "hidup" untuk batas waktu tertentu sebelum ia meluruh, dan rerata waktu hidup adalah rerata aritmatika dari keseluruhan waktu hidup atom-atom material tersebut. Rerata waktu hidup disimbolkan dengan

\tau

, dan mempunyai hubungan dengan konstanta peluruhan sebagai berikut:

\tau = \frac{1}{\lambda}

Parameter yang lebih biasa digunakan adalah waktu paruh. Waktu paruh adalah waktu yang diperlukan sebuah inti radioatif untuk meluruh menjadi separuh bagian dari sebelumnya. Hubungan waktu paruh dengan konstanta peluruhan adalah sebagai berikut:

t_{1/2} = \frac{\ln 2}{\lambda}

Hubungan waktu paruh dengan konstanta peluruhan menunjukkan bahwa material dengan tingkat radioaktif yang tinggi akan cepat habis, sedang materi dengan tingkat radiasi rendah akan lama habisnya. Waktu paruh inti radioaktif sangat bervariasi, dari mulai 10²⁴ tahun untuk inti hampir stabil, sampai 10^-6 detik untuk yang sangat tidak stabil.

Contoh Soal UN Efek Foto Listrik

Cermati gambar percobaan penyinaran suatu lempeng logam dengan cahaya berikut. Jika fungsi kerja logam adalah 2,2 eV dan cahaya yang disinarkan memiliki panjang gelombang λ dan frekuensi f tentukan:

a) energi cahaya minimal yang diperlukan agar elektron lepas dari logam
b) frekuensi cahaya minimal yang diperlukan agar elektron lepas dari logam
c) panjang gelombang maksimum yang diperbolehkan agar elektron lepas dari logam
Gunakan data berikut :
Cepat rambat cahaya c = 3 x 108 m/s
Tetapan Planck h = 6,6 x 10−34 Js
1 eV = 1,6 x 10−19 joule

Pembahasan
a) energi cahaya minimal yang diperlukan agar elektron lepas dari logam
energi cahaya minimal tidak lain adalah energi ambang atau fungsi kerja logam. Sehingga
Wo = 2,2 eV
Wo = 2,2 x (1,6 x 10−19 ) joule = 3,52 x 10−19 joule

b) frekuensi cahaya minimal yang diperlukan agar elektron lepas dari logam
Ingat energi foton atau cahaya adalah E = hf, E disini dilambangkan sebagai Wo sehingga
Wo = h fo
3,52 x 10−19 = 6,6 x 10−34 x fo
fo = 0,53 x 1015 joule

c) panjang gelombang maksimum yang diperbolehkan agar elektron lepas dari logam
Hubungkan dengan kecepatan cahaya
λmax = c / fo
λmax = 3 x 108 / 0,53 x 1015
λmax = 5,67 x 10−7 m

Soal No. 2
Cermati gambar percobaan penyinaran suatu lempeng logam dengan cahaya berikut:

Jika fungsi kerja logam adalah 2,1 eV dan cahaya yang disinarkan memiliki panjang gelombang 2500 Å dengan konstanta Planck 6,6 x 10−34 Js dan 1 eV = 1,6 x 10−19 joule, tentukan
a) energi ambang logam dalam satuan joule
b) frekuensi ambang
c) panjang gelombang maksimum yang diperlukan untuk melepas elektron dari logam
d) panjang gelombang dari cahaya yang disinarkan dalam meter
e) frekuensi dari cahaya yang disinarkan dalam Hz
f) energi foton cahaya yang disinarkan
g) energi kinetik dari elektron yang lepas dari logam

Pembahasan
Skemanya seperti ini

Logam yang di dalamnya terdapat elektron-elektron disinari oleh cahaya yang memiliki energi E. Jika energi cahaya ini cukup besar, maka energi ini akan dapat melepaskan elektron dari logam, dengan syarat, energi cahayanya lebih besar dari energi ambang bahan. Elektron yang lepas dari logam atau istilahnya fotoelektron akan bergerak dan memiliki energi kinetik sebesar Ek

Hubungan energi cahaya yang disinarkan E, energi ambang bahan Wo dan energi kinetik fotoelektron Ek adalah
E = Wo + Ek
atau
hf = hfo + Ek

a) energi ambang logam dalam satuan joule
Wo = 2,1 x (1,6 x 10−19 ) joule = 3,36 x 10−19 joule

b) frekuensi ambang
Wo = h fo
3,36 x 10−19 = 6,6 x 10−34 x fo
fo = 0,51 x 1015

c) panjang gelombang maksimum yang diperlukan untuk melepas elektron dari logam
λmax = c / fo
λmax = 3 x 108 / 0,51 x 1015
λmax = 5,88 x 10−7 m d) panjang gelombang dari cahaya yang disinarkan dalam meter
λ = 2500 Å = 2500 x 10−10 m = 2,5 x 10−7 m

e) frekuensi dari cahaya yang disinarkan dalam Hz
f = c/λ
f = 3 x 10 8/2,5 x 10−7
f = 1,2 x 10 15 Hz

f) energi cahaya yang disinarkan
E = hf
E = (6,6 x 10−34) x 1,2 x 10 15 = 7,92 x 10 −19 joule

g) energi kinetik dari elektron yang lepas dari logam
E = Wo + Ek 7,92 x 10 −19 = 3,36 x 10−19 + Ek
Ek = 7,92 x 10 −19 − 3,36 x 10−19 = 4,56 x 10−19 joule

Soal No. 3
Sebuah keping logam yang mempunyai energi ambang 2 ev disinari dengan cahaya monokromatis dengan panjang gelombang 6000 Å hingga elektron meninggalkan permukaan logam. Jika h = 6,6 × 10−34 Js dan kecepatan cahaya 3 × 108 m/detik, maka energi kinetik elektron yang lepas....
A. 0,1 × 10–19 joule
B. 0,16 × 10–19 joule
C. 1,6 × 10–19 joule
D. 3,2 × 10–19 joule
E. 19,8 × 10–19 joule
Sumber soal : Ebtanas tahun 1986

Pembahasan
Data dari soal:
Energi ambang Wo = 2 eV = 2 x (1,6 x 10−19 ) = 3,2 x 10−19joule
Panjang gelombang λ = 6000 Å = 6000 x 10−10 = 6 x 10−7 m

Menentukan energi kinetik foto elektron:

Soal No. 4
Permukaan katode disinari cahaya sampai pada frekuensi tertentu, ternyata tidak terjadi foto elektron. Agar permukaan katode memancarkan foto elektron, usaha yang dapat dilaksanakan adalah …
A. mengurangi tebal katode dan memperbesar intensitas cahaya
B. memperbesar panjang gelombang dan memperbesar intensitasnya
C. mengurangi tebal katode dan memperbesar panjang gelombang
D. memperbesar frekuensi cahaya sampai frekuensi batas dan memperbesar intensitasnya
E. memperbesar frekuensi cahaya sampai di atas frekuensi batas dan memperbesar intensitasnya
Sumber soal : Ebtanas 1987

Pembahasan
Foto elektron tidak terjadi berarti energi cahaya yang disinarkan masih dibawah energi ambang, untuk itu frekuensi cahaya harus diperbesar hingga menghasilkan energi yang melebihi energi ambang. Untuk memperbanyak jumlah foto elektron yang terjadi, maka intensitas cahaya harus dinaikkan.

Soal No. 5
Hubungan energi kinetik elektron dan frekuensi penyinaran pada gejala foto listrik terlihat pada grafik di bawah ini.

Apabila konstanta Planck h, besarnya fungsi kerja logam adalah …
A. 1 h
B. 2 h
C. 3 h
D. 4 h
E. 8 h
Sumber soal : Ebtanas 1989

Pembahasan
Dari gambar terlihat frekuensi ambang adalah 4 HZ, sehingga nilai fungsi kerja logam
Wo = hfo = h(4) = 4h

Soal No. 6
Cahaya dengan panjang gelombang 500 nm meradiasi permukaan logam yang fungsi kerjanya 1,86 × 10–19 joule. Energi kinetik maksimum foto elektron adalah …
A. 2 × 10–19 joule
B. 4 × 10–19 joule
C. 5 × 10–19 joule
D. 6 × 10–19 joule
E. 9 × 10–19 joule
Sumber soal : Ebtanas 1990

Pembahasan

Data dari soal sebagai berikut:
λ = 500 nm = 500 x 10–9 m = 5 x 10–7 m
Wo = 1,86 x 10–19
Ek = ....?

Soal No. 7
Frekuensi ambang suatu logam sebesar 8 × 1014 Hz, dan logam tersebut disinari dengan cahaya yang mempunyai frekuensi 1015 Hz. Jika tetapan Planck = 6,6 × 10–34 J s, maka energi kinetik foto elektron yang terlepas dari permukaan logam tersebut adalah …
A. 1,32 × 10–19 joule
B. 1,32 × 10–19 joule
C. 1,32 × 10–19 joule
D. 1,32 × 10–19joule
E. 1,32 × 10–19 joule
Sumber soal : Ebtanas 1991

Pembahasan
Data yang diberikan oleh soal:
frekuensi ambang fo = 8 × 1014 Hz
frekuensi cahaya f = 1015 = 10 × 1014 Hz
Ek = ...?

Soal No. 8
Frekuensi ambang natrium adalah 4,4 x 1014 Hz. Besar potensial penghenti dalam volt bagi natrium saat disinari dengan cahaya yang frekuensinya 6,0 x 1014 Hz adalah...
A. 0,34
B. 0,40
C. 0,44
D. 0,66
E. 0,99
Sumber soal : UMPTN 1999

Pembahasan
Data dari soal:
f = 6,0 x 1014 Hz
fo = 6,0 x 1014 Hz
Potensial penghenti = ...?
Ek = h(f−fo)
Ep = qV
dimana muatan elektron adalah 1,6 x 10−19 Coulomb

Contoh Soal UN Kapasitor

Selasa, 03 Maret 2015

Soal No. 1
Perhatikan gambar berikut, 3 buah kapasitor X, Y dan Z disusun seperti gambar. Jika saklar S ditutup tentukan :
a) Nilai kapasitas kapasitor pengganti rangkaian
b) Muatan yang tersimpan dalam rangkaian
c) Muatan yang tersimpan dalam kapasitor Z menurut prinsip rangkaian seri
d) Beda potensial ujung-ujung kapasitor Z
e) Beda potensial ujung- ujung kapasitor X
f) Beda potensial ujung-ujung kapasitor Y
g) Muatan yang tersimpan pada kapasitor X
h) Muatan yang tersimpan pada kapasitor Y
i) Muatan yang tersimpan pada kapasitor Z
j) Energi yang tersimpan dalam rangkaian
k) Energi yang tersimpan pada kapasitor X
l) Energi yang tersimpan pada kapasitor Y
m) Energi yang tersimpan pada kapasitor Z

(Sumber gambar dan angka : Soal Ujian Nasional Fisika SMA 2007/2008)

Pembahasan
a) Paralel antara kapasitor X dan Y didapatkan kapasitor ekivalennya namakan Cxy :

Sekarang rangkaian menjadi lebih sederhana yaitu terdiri dari Cxy yang diseri dengan Cz yang menghasilkan kapasitas pengganti namakan Ctot :

b) Muatan yang tersimpan dalam rangkaian namakan Qtot

c) Muatan yang tersimpan dalam kapasitor Z namakan Qz

Untuk rangkaian kapasitor seri berlaku :

d) Beda potensial ujung-ujung kapasitor Z namakan Vz

e) Beda potensial ujung-ujung kapasitor X dan kapasitor Y adalah sama karena dirangkai paralel

f) Beda potensial ujung-ujung kapasitor Y sama dengan X

g) Muatan yang tersimpan pada kapasitor X saja (bukan gabungan antara X dan Y, sehingga hasilnya tidak akan sama dengan Ctot)

h) Muatan yang tersimpan pada kapasitor Y

i) Muatan yang tersimpan pada kapasitor Z

j) Energi yang tersimpan dalam rangkaian

Rumus umum untuk menghitung energi pilih salah satu

Sehingga

k) Energi yang tersimpan pada kapasitor X

l) Energi yang tersimpan pada kapasitor Y

m) Energi yang tersimpan pada kapasitor Z

Soal No. 2
Diberikan susunan 3 buah kapasitor yang dipasang pada sumber 24 Volt seperti gambar berikut!

Jika saklar S ditutup, tentukan :
a) Nilai kapasitas kapasitor pengganti rangkaian
b) Muatan yang tersimpan dalam rangkaian
c) Muatan yang tersimpan dalam kapasitor Z
d) Beda potensial ujung-ujung kapasitor Z
e) Beda potensial ujung-ujung kapasitor X
f) Beda potensial ujung-ujung kapasitor Y
g) Muatan yang tersimpan pada kapasitor X
h) Muatan yang tersimpan pada kapasitor Y
i) Energi yang tersimpan dalam rangkaian
j) Energi yang tersimpan pada kapasitor X
k) Energi yang tersimpan pada kapasitor Y
l) Energi yang tersimpan pada kapasitor Z

Silahkan mencoba,..!!

Soal No. 3
Kapasitor keping sejajar dengan luas penampang masing-masing keping adalah 50 cm2 tanpa bahan pengisi (berisi udara). Jarak antar keping adalah 2 cm dan kedua keping diberi beda potensial 120 volt. Jika εo adalah 8,85 x 10− 12 C2N − 1 − 2 tentukan :
a) kapasitas kapasitor
b) muatan yang tersimpan dalam kapasitor
c) kuat medan listrik antara kedua keping

Pembahasan
a) kapasitas kapasitor

b) muatan yang tersimpan dalam kapasitor

c) kuat medan listrik antara kedua keping

Soal No. 4
Sebuah kapasitor keping sejajar memiliki kapasitas sebesar C. Jika kapasitor disisipi bahan dielektrik dengan konstanta dielektrik sebesar 2, tentukan kapasitasnya yang baru!

Pembahasan
Luas penampang dan jarak keping kapasitor tidak mengalami perubahan:

Soal No. 5
Sebuah kapasitor keping sejajar memiliki kapasitas 1200 μF. Jika luas penampang keping dijadikan dua kali semula dan jarak antar keping dijadikan 1,5 kali semula, tentukan nilai kapasitasnya yang baru!

Pembahasan

Soal No. 6
Kapasitor bola berongga memiliki jari-jari sebesar 1,8 cm. Jika 1/4πεo = 9 x 109 dalam satuan internasional, tentukan kapasitas kapasitor!

Pembahasan
Kapasitas kapasitor bola denganjari-jari R :

Soal No. 7
Tiga kapasitor yang masing-masing kapasitasnya 3 F, 6 F, dan 9 F dihubungkan seri. Kedua ujung dari gabungan tersebut dihubungkan dengan sumber tegangan yang besarnya 220 V. Tegangan antara ujung-ujung kapasitor yang 3 F adalah....
A. 40 V
B. 60 V
C. 110 V
D. 120 V
E. 220 V
(Soal SKALU 1978)

Pembahasan
Menentukan tegangan kapasitor pada susunan seri.

Cara Pertama
Cari kapasitas gabungan ketiga kapasitor terlebih dahulu:
1/Cgab = 1/C1 + 1/C2 + 1/C3
1/Cgab = 1/3 + 1/6 + 1/9
1/Cgab = 6/18 + 3/18 + 2/18
1/Cgab = 11 / 18
Cgab = 18/11 Farad

Cari muatan gabungan:
Qgab = Cgab Vgab
Qgab = (18/11) × 220 = 360 Coulomb

Pada suatu rangkaian kapasitor seri seperti gambar di atas, berlaku Q1 = Q2 = Q3 = Qgab, sehingga nilai Q1 = 360 Coulomb

Tegangan pada C1
V1 = Q1 / C1
V1 = 360 / 3 = 120 volt

Cara Kedua
Dengan perbandingan untuk pembagian tegangan pada susunan kapasitor seri:

                       1         1    1
V1 : V2 : V3 = ____ : _____ : _____
                       C1   C2        C3

                       1        1    1
V1 : V2 : V3 = ____ : _____ : _____
                      3         6 9
Perbandingan yang didapat dalam pecahan yaitu 1/3, 1/6 dan 1/9, untuk perhitungan lebih mudah dalam angka non pecahan, untuk itu kalikan masing-masing dengan sebuah angka yang sama, disini dikali angka 18 sehingga didapat perbandingan ekivalennya:

V1 : V2 : V3 = 6 : 3 : 2

Untuk V1,
                   6
V1 = ________________ × Vgab
           (6 + 3 + 2)

             6
V1 = ________ × 220 = 120 volt
            11

Tegangan pada kapasitor 3 F adalah 120 V

Jika ingin V2 maka:

               3
V2 = ________________ × Vgab
           (6 + 3 + 2)

               3
V2 = ________ × 220 = 60 volt
           11

Dengan cara yang sama bisa dicari V3.

About me

Archivo del blog